Vacuum Coffee Pots: Physics

THE PHYSICS OF VACUUM POTS
The operation of a vacuum coffee pot is a source of considerable fascination, but the physical processes involved are often not clearly understood. The following is an attempt to demystify the physics of the vacuum brewing process.

T = 294 K
Va = 0.237 liters

Step 1: When the vacuum pot is assembled, we have an essentially closed (air-tight) lower chamber which contains water and, in the space above the water, a mixture of air and water vapor. The concentration of water vapor depends only on the temperature. It is not dependent on the quantity of water and is only slightly influenced by the presence of the air in the chamber.
The total pressure (Pt) inside the lower chamber is a combination of the pressure exerted by the air (air pressure) and by the water vapor (vapor pressure).
The air pressure (Pa) exerted on the walls of the container and on the surface of the water is expressed by the Ideal Gas Law, which approximates the behavior of ideal gases at low pressures:
*Pa = nRT / V*	where Pa is air pressure (atm) V is Volume (liters) n is quantity of gas (moles) R is the universal gas constant T is temperature (K)
If we assume a starting condition of the vacuum pot with its lower chamber filled with water to seven-eighths capacity, and an air pressure (Pa) at room temperature (294K) of 1 atm, we can estimate the quantity of air inside the lower chamber:
PV = nRT n = PaVa/RT n = (1 atm) (0.237 liters) / (0.0821 liter-atm/mole-K) (294 K) n = 0.00982 moles
The vapor pressure (Pv) at the starting point is essentially zero.
Pv = 0 atm
The total pressure in the lower chamber is the sum of the air pressure (Pa) and the vapor pressure (Pv). At room temperature (294K), this yields the following:
Pa = 1 atm Pv = 0 atm Pt = Pa + Pv = 1 atm + 0 atm = 1 atm

T = 363 K
Va = 0.828 liters

Step 2:
As heat is added to the system, several changes begin to occur. In the lower chamber, a saturated condition develops and the vapor pressure (Pv) exerted on the walls of the container and on the surface of the water increases exponentially with temperature. The saturated vapor pressure can be approximated by the equation [F. W. Murray, 1966] :

Pv = 0.006 · exp[ a · (T - 273.16) / (T - b)]

where
Pv is vapor pressure (atm)
a is the constant 17.27 over water
b is the constant 35.86 over water
T is temperature (K)

At about 353K, air dissolved in the water starts to be released as tiny bubbles and the air and water vapor over the surface of the water increase in temperature. When the total pressure (Pt) exceeds the external air pressure (1 atm), the force on the surface of the water inside the lower chamber is greater than the force on the surface of the water in the funnel tube and upper chamber. As a result, water from the lower chamber is gradually forced up the funnel tube into the upper chamber where it mixes with the ground coffee. The greater the total pressure, the higher the water rises. [Note that we have chosen to ignore any resistance from the ground coffee or filtering mechanism.]

If we use the temperature of the water half-way down the funnel tube to approximate the temperature of the whole system, we can calculate the total pressure (Pt) in the chamber as a function of temperature. Experimental measurements of the water temperature (T) and corresponding gas volume (V) in the chamber yield the following:

T (K)	V (l)
298	0.237
303	0.242
308	0.247
313	0.248

T (K)	V (l)
318	0.266
323	0.274
328	0.286
333	0.300

T (K)	V (l)
338	0.307
343	0.319
348	0.367
353	0.414

T (K)	V (l)
358	0.532
363	0.828
368	1.064
373	1.419

Remembering that the total pressure (Pt) is the sum of the air pressure (Pa) and vapor pressure (Pv), we can now estimate the total pressure at any point in the process after saturation has occurred. For example, at 363K:

Pa = nRT/Va
Pa = (0.0107 moles)(0.0821 liter-atm/mole-K)(363 K) / (0.828 liters) = 0.389 atm

Pv = 0.006 · exp[ a · (T - 273.16) / (T - b)]
Pv = 0.006 · exp[ 17.27 · (363 - 273.16) / (363 - 35.86)] = 0.698 atm

Pt = Pa + Pv = 0.389 atm + 0.698 atm = 1.087 atm

Throughout this process, the system remains in dynamic equilibrium, with increasingly more liquid water escaping as vapor (due to the increase in kinetic energy resulting from the increase in temperature) and vapor condensing back into liquid water at an equivalent rate.

T = 368 K
Va = 1.064 liters

Step 3:
As the total pressure (Pt) continues to increase, the volume of water in the lower chamber decreases and the volume of gas increases until the water's surface reaches the bottom of the funnel tube. The temperature measured experimentally at this stage was 368K.

Up to this point, the quantity of water vapor and the associated vapor pressure in the chamber has steadily increased, but the quantity of air molecules has remained essentially constant (it's an air-tight system). Remembering that the quantity of air calculated in Step 1 was 0.0097 moles, and allowing for an estimated 10%** increase in air molecules due to the release of air dissolved in the water (0.0097 moles x 1.10 = 0.0107 moles), we can estimate the air pressure (Pa) at 368K:

PV = nRT
Pa = nRT/Va
Pa = (0.0107 moles)(0.0821 liter-atm/mole-K)(368 K) / (1.064 liters)
Pa = 0.304 atm

The air pressure (Pa) in the system has actually decreased to about one third it's starting value, and therefore can not be the dominant force in the vacuum brewing process. The increase in volume in the lower chamber has effectively canceled out any pressure gains produced by the increased temperature.

Calculating vapor pressure at this point reveals the greater force behind the brewing process:

Pv = 0.006 · exp[ a · (T - 273.16) / (T - b)]
Pv = 0.006 · exp[17.27 · (368 - 273.16) / (368 -35.86)] atm
Pv = 0.842 atm

Again, the total pressure (Pt) is the combination of the two:

Pt = Pa + Pv
Pt = 0.304 atm + 0.842 atm
Pt = 1.146 atm

This pressure exceeds the external pressure (1 atm) and is sufficient to force the water up the funnel tube.

** This estimate is based on the combined solubility of the three primary constituents of air in water at 1 atm, weighted according to their relative percentages: Nitrogen (79%), Oxygen (20%) and Argon (1%).

T = 373 K
Va = 1.419 liters

Step 4:
As we continue to heat the system, the total pressure (Pt) forces the surface of the water in the lower chamber below the bottom of the funnel tube. At this point the system is no longer closed. The pressurized gas in the lower chamber is allowed to escape and it bubbles up through the liquid in the upper chamber. The escaping gases include both air and water vapor, resulting in a net decrease in the quantity of air in the lower chamber.

We can calculate the theoretical maximum total pressure (Pa) at Step 4:

Pa = (0.0107 moles)(0.0821 liter-atm/mole-K)(373 K) / (1.419 liters) = 0.231 atm
Pv = 0.006 · exp[17.27 · (373 - 273.16) / (373 -35.86)] atm = 1 atm
Pt = 0.231 atm + 1 atm
Pt = 1.231 atm

At this point in the process, the water in the lower chamber begins to boil. Large bubbles of water vapor rise and break the surface of the water. In the normal brewing process, the heat is lowered at this point and the whole system is allowed to "gurgle" for several minutes. This further reduces the amount of air in the lower chamber as air molecules are pushed out and replaced by water vapor. The amount of air removed during this process depends on the length of time that the system is allowed to "gurgle". 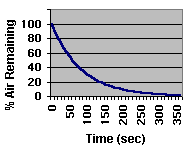By estimating the bubble size and escape rate, and assuming good mixing of the gases and an exponential decay of air (as a percentage of the total volume of gases) over time, we can calculate the amount of air remaining in the lower chamber as a function of "gurgle" time.

Gurgle Time	Percent of Air Remaining
1 minute	49%
2 minutes	25%
3 minutes	12%
4 minutes	6%
5 minutes	3%

ExponentialDecay.gif (1564 bytes)

In order for a sufficient vacuum to form to complete the brewing process, it appears that the ratio of air to water vapor achieved during the "gurgling" process must reach a specific value. The quantity of air molecules at the starting point varies directly with the initial water level -- the less water used, the more air in the chamber. As a result, a longer or shorter "gurgle" time is required to reach the critical air/vapor ratio, depending on the starting water level. Experimental results show the maximum allowable quantity of post-gurgle air molecules to be approximately 0.005 moles. This allows us to suggest minimum gurgle times for different initial water levels for an 8-cup vacuum pot:

Starting Water Level	Air Molecules (initial)	Air to Vapor Reduction Req'd	Minimum Estimated Gurgle Time
7/8 full	0.00982 moles	49%	1 minute
2/3 full	0.0196 moles	74%	2 minutes
1/2 full	0.343 moles	85%	3 minutes

Click here for comparative plots of Pressure as a function of "gurgle" time.

It should be remembered that the force of the vacuum must also overcome any resistance caused by the ground coffee and filter mechanism. Since this varies so widely with the fineness of the grind and the design of the fiter, we are forced to ignore this factor in our calculations.

In this model, we will assume a two minute gurgle time and a corresponding 75 percent reduction in air molecules during the time span that the system remains open such that Va (final) = 0.25 Va (initial).

Note: The increase in pressure inside the lower chamber elevates the boiling point of the water by about 1 degree K for each 28 mmHg (0.0037 atm), which in our case would result in a theoretical boiling point of about 378K. But since boiling generally occurs only after the system has become open (at which point the actual pressure in the lower chamber is difficult to determine), this factor has been ignored in this model.

T < 373 K
Va < 1.419 liters

Step 5:
After two minutes of "gurgling", the heat is removed from the system and the gases in the lower chamber begin to cool. As a result, the volume of air decreases and the water vapor begins to condense to liquid more quickly than the water evaporates to vapor. Consequently, the total internal pressure decreases. When the internal pressure falls below the external pressure (1 atm), the water in the upper chamber is forced back down the funnel tube into the lower chamber.

We can calculate the approximate temperature at which the downward flow begins.

Pt = Pa + Pv = 1 atm
Pa = nRT/Va
Pv = 0.006 · exp[ a · (T - 273.16) / (T - b)]
nRT/Va + 0.006 · exp[ a · (T - 273.16) / (T - b)] = 1 atm
solving for T, we find:
T = 369 K

As soon as the water level in the lower chamber rises above the bottom of the funnel tube, the system becomes closed once again. As the temperature continues to drop, the water vapor condenses rapidly, causing the total internal pressure (Pt) to drop precipitously. The difference between the internal and external pressures results in the formation of a partial vacuum within the lower chamber, and the higher external pressure forces the brewed coffee rapidly into the lower chamber.

T = 353 K
Va = 0.237 liters

Step 6:
When all the brewed coffee has been pushed down into the lower chamber there may still be sufficient vacuum in the lower chamber to force a quantity of air down the funnel tube as well, with air bubbles visibly rising from the bottom of the funnel.

We can calculate the approximate total pressure just as the coffee has completely returned to the lower chamber:

Pa = (0.0107 moles)(0.25)(0.0821 liter-atm/mole-K)(353 K) / (0.237 liters)
Pv = Pv = 0.006 · exp[17.27 · (353 - 273.16) / (353 -35.86)] atm
Pt = Pa + Pv
Pt = 0.327 atm + 0.470 atm = 0.797 atm

At this point, the pressure in the lower chamber is still substantially lower than the external air pressure of 1 atm as predicted. The bubbling of air partially equalizes the internal and external pressures, but can not succeed completely due to the work required to push the air bubbles down the tube.

T = 348 K
Va = 0.237 liters

Step 7:
At the end of the process, all the coffee has returned to the lower chamber, and some of the difference between the internal and external pressures has been equalized. The process ends with a small but perceptible vacuum in the lower chamber, requiring a slight effort to remove the upper chamber.

To review, it is the combination of air pressure and vapor pressure that work together to push the water upward in the first stage of the vacuum brewing process, but it is primarily the condensation or phase change of the water vapor which creates the partial vacuum, and thereby triggers the second stage.

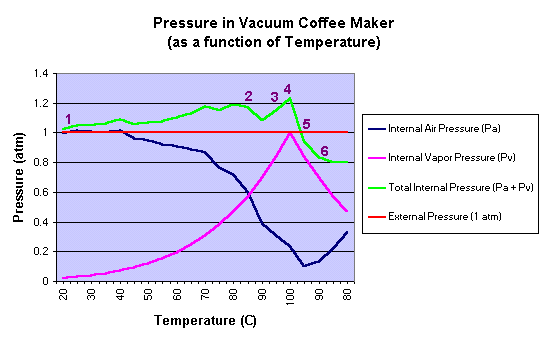
Process Overview:
It may be interesting to inspect a plot of the pressures involved in the vacuum brewing process as a function of temperature. The plot shown below is based upon a model developed from the equations and approximations described above.

Rubberless Vacuum Brewers:
Brewing coffee in one of the "rubberless" (i.e. gasket-less) vacuum brewers poses special consideration to one wishing to understand the physics of the vacuum coffee pot. In these brewers there is no rubber gasket to form an air-tight seal between the upper and lower chambers. 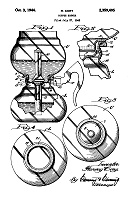Instead, the combined weights of the upper chamber, filter, and ground coffee must be sufficient to counter the total internal pressure exerted upward which would tend to dislodge the upper chamber. Here is how the inventor, Harvey Cory, explained it:

"The seal provided by the ground joint is maintained fluid tight by the weight of the upper bowl plus the rod. The pressure developed during the brewing operation tends to lift the upper bowl and break the seal. This pressure is determined by the height the water must rise before its weight in the upper bowl more than compensates for the additional difference in levels. In the case of an upper bowl of eight-cup capacity (about 46 ounces), its weight, plus that of the rod, may be about 14 to 15 ounces, and with the ground coffee therein, the total weight is about .95 pound. The height to which the water must rise depends upon the amount thereof which is displaced from the lower bowl. Under ordinary conditions this may require a head of from two and a half to three and a half inches. If the mean diameter of the sealing surfaces is X inches, then the value X for the pressure conditions will have to be balanced will be as follows:

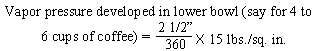
For balanced condition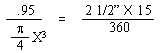

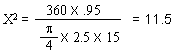
eq4.gif (426 bytes)

"This figure of 3.4 inches diameter which is theoretical requires that some factor of safety be allowed. For instance, it is found that with the rod and ground coffee in place, some restriction is offered to the up-flow of water into the upper bowl. This will increase the effective internal pressure required to raise the water into the upper bowl. There is also the weight pressure which must overbalance the internal pressure by a small amount in order that the seal may remain fluid tight. For these reasons, two and seven-eighths inches represents a practical maximum value for the X dimension in the case of a coffee maker of the size indicated."

[Excerpt from U.S. Patent No. 2359405, dated Oct. 3, 1944]